报告题目：An Efficient Semismooth Newton Method for Adaptive Sparse Signal Recovery Problems

报告人：河南大学，肖运海教授

报告时间：2021年11月4日 10:30-

报告地点：腾讯会议339 800 438

报告摘要：

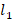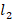We know that compressive sensing can establish stable sparse recovery results from highly undersampled data under a restricted isometry property condition. In reality, however, numerous problems are coherent, and vast majority conventional methods might work not so well. Recently, it was shown that using the difference between and -norm as a regularization always has superior performance. In this talk, we propose an adaptive 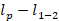model where the -norm with 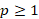measures the data fidelity and the 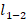-term measures the sparsity. This proposed model has the ability to deal with different types of noises and extract the sparse property even under high coherent condition. We use a proximal majorization-minimization technique to handle the nonconvex regularization term and then employ a semismooth Newton method to solve the corresponding convex relaxation subproblem. We prove that the sequence generated by the semismooth Newton method admits fast local convergence rate to the subproblem under some technical assumptions. Finally, we do some numerical experiments to demonstrate the superiority of the proposed model and the progressiveness of the proposed algorithm. This is a joint work with Yanyun Ding and Haibin Zhang from Beijing University of Technology, and Peili Li from East China Normal University.

报告人简介：

肖运海，河南大学教授、博士生导师，省特聘教授，2007年在湖南大学获博士学位，研究方向为最优化算法及应用。在Math. Prog. Comput., Comput. Opt. Appl.等期刊发表论文50余篇，主持国家自然科学基金3项。兼任中国工业与应用数学会理事、中国工业与应用数学会青年工作委员会副主任、中国运筹学会宣传工作委员会副主任、河南省运筹学会副理事长、河南大学学术委员会委员、《数学季刊》编辑部主任等。